介绍
在本文中,我们提出了一种不基于物理或数学特征的自然图像反卷积方法,我们展示了使用图像样本构建数据驱动系统的新方向,这些图像样本可以很容易地从摄像机中生成或在线收集。
我们使用卷积神经网络(CNN)来学习反卷积操作,不需要知道人 为视觉效果产生的原因,与之前的基于学习的图像去模糊方法不同,它不依赖任何预处理。本文的工作是在反卷积的伪逆背景下,我们利用生成模型来弥补经验决定的卷积神经网络与现有方法之间的差距。我们产生一个实用的系统,提供了有效的策略来初始化网络的权重值,否则在卷积随机初始化训练过程中很难得到,实验证明,当输入的模糊图像是部分饱和的,我们的系统比之前的方法效果都要好。
模糊退化
图像模糊往往由多种因素导致,如:剪强度(饱和度),相机噪声,压缩等,定义如下模糊模型:
ˆ y = ψb[φ(αx ∗ k + n)],
αx表示潜在的清晰图像,符号α≥1表示αx可能值超过相机传感器的动态范围,因此被省略。k为卷积核,通常被称为点扩展函数(PSF),n为模型添加的相机噪声,φ(·)是饱和限幅函数模型,定义 φ(z) = min(z,zmax), zmax是阈值范围,ψb[·] 是非线性(如JPEG)压缩操作。
即使我们知道 ˆ y 和k,想要复原αx还是比较困难,因为在剪裁的时候会有信息损失,所以我们的目标是复原剪裁过的输入ˆ x,其中ˆ x = φ(αx)。
尽管求解ˆ x和一个复杂的能量函数涉及到上面的公式很困难,从输入图像x得到模糊图像比较简单,根据卷积模型将各种可能的图像退化转化为生成来合成图像,这激发了反卷积的学习过程,训练图像对{ˆ xi,ˆ yi}。
分析
我们的目标是训练一个网络结构 f(·) ,使得下面式子最小: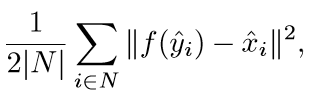
|N|为样本集中图像对的个数。
我们已经使用了最近的两种深度神经网络来解决这个问题,但都不成功。其中一个是 Stacked Sparse Denoise Autoencoder (SSDAE) ,另一个为卷积神经网络(CNN),这两种方法都是为了图像去噪设计的,对于SSDAE,我们选择patch大小为17*17。在训练中,我们收集了两百万个清晰的patch及对应的模糊版本。其中一个例子如下:
从图上看到,SSDAE的结果仍然比较模糊,CNN的效果稍微好一些,但它仍有模糊的边缘和强烈的重影痕迹,这是因为这些网络结构是为了去噪,而没有考虑到反卷积性质。
Pseudo Inverse Kernels(伪逆内核)
假设线性模糊模型为:y = x ∗ k
空间卷积可以转化为频域乘法:F(y) = F(x) · F(k).
其中F(·)表示离散傅里叶变换(DFT), 操作符 · 是元素相乘。在傅里叶域中,x可以表示为: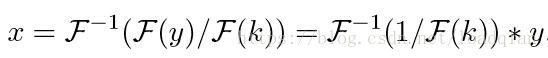
其中,F−1为逆离散傅里叶变换。x的解写成一种空间卷积,核为 F−1(1/F(k)), 内核实际上是一个在没有紧支柱的情况下跨越整个空间域的重复信号。当噪声出现时,通常使用正则化项来避免频域中除数为零,使得伪逆在空间域中快速衰减。
经典的维纳反卷积相当于使用Tikhonov正则化矩阵。维纳反卷积如下: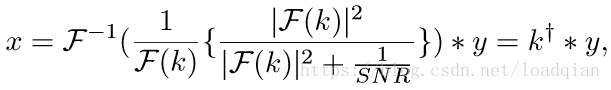
SNR为信噪比,k+为伪逆核,噪声越大,1/SNR就越大。下图(a)显示了一个半径为7的磁盘模糊核,通常用于焦模糊模型。下图(b)是伪逆核k+且SNR=1E-4,一张使用此模糊核的图像如图(c),k+结合反卷积的结果如图(d)。这种方法可以去掉一部分图像中的模糊,但是噪声和饱和会引起视觉伪影,这与我们对维纳反卷积的理解是一致的。总结来说,使用深度卷积网络来做图像反卷积其实并不简单,增加卷积核来简单地修改网络结构会导致训练难度增加,我们采用一种新的结构来改进网络,结果如图(e)。
网络结构
基于核可分性定理,将反卷积的伪逆核转化为卷积网络。它使网络具有更强的表现力,映射到更高的维度以适应非线性特征。
核可分性定理
核可分性是通过奇异值分解(SVD)来实现的,给定伪逆核k+,可以分解为k+=USV T ,用uj,vj分别表示U和V的第j列,sj为第j个奇异值,原始的伪反卷积课表示为: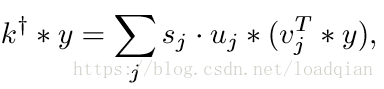
二维卷积可以看成是一维滤波器的加权和。在实验中,近似地将k+看成一个可分的滤波器,将核与接近0或者非常小的sj相关联,我们尝试使用真正的模糊核来忽略小于0.01的奇异值,得到的可分离核的平均值维30。使用的SNR越小,逆核的空间支持就越小,我们还发现,长度为100的逆核通常足以产生看似合理的反卷积结果,这一点对我们设计网络的结构非常重要。
图像反卷积神经网络(DCNN)
这个网络可以表示为: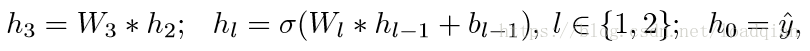
其中,Wl是第(l-1)层到第l层的权值映射,b l-1为偏差。σ(·) 为非线性函数,可以是 sigmoid 或者tanh。
我们的网络包含两个隐藏层,类似于可分离核的反转设置。第一个隐藏层h1使用38个大规模一维核,大小为121*1.第二个隐藏层h2使用38个 1*121的卷积核对应着h1中的38个映射。为了产生结果,使用一个1*1*138的核,类似于使用奇异值sj的线性组合。
优点:(1)它聚集了可分离核反转进行反卷积,因此保证是最优的;(2)非线性特征和高维度结构使得网络比传统的伪逆结构更具有表现力。
训练DCNN
我们都自然图像采取两种策略进行实验,添加高斯噪声(AWG)和JPEG压缩技术,分为两类:一类具有强烈的色相饱和度,一类没有。饱和度影响了许多现有的反卷积算法。PSNR如图: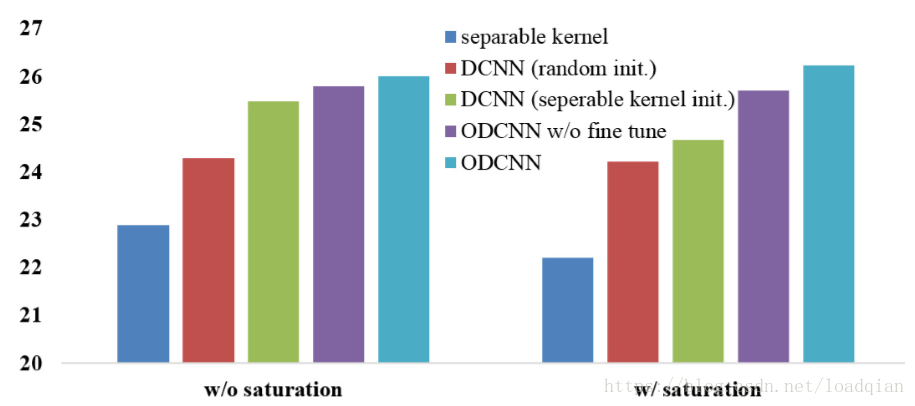
从图中可以得出两点:
(1)训练后的网络比简单地执行可分离核反演具有优势,无论是随机初始化还是使用伪逆初始化。而且高维度映射和非线性特征是我们的网络比简单的可分离核反演更具表现力。
(2)使用可分离核反演初始化的PSNR值比随机初始化后的更高,表明初始值会对网络产生影响,因此要进行调优。
其视觉比较如下:
其中,(a)-(c)是可分离核反演,使用随机初始化权重和可分离反转初始化,图(c)明显包含更多的边缘和细节特征,最后的DCNN并不等同于任何现有的反核函数,即使有各种正则化,因为它涉及到具有非线性的高维映射。
在彩色饱和的图像中,CNN的反卷积性能降低,由于噪声和压缩,视觉伪影也可能产生,接下来,我们将通过合并一个消除噪声的CNN模块,转向更深层次的结构来解决这些遗留的问题。
Outlier-rejection Deconvolution CNN (ODCNN)
完整的网络结构是将反卷积CNN与去噪CNN结合,如下: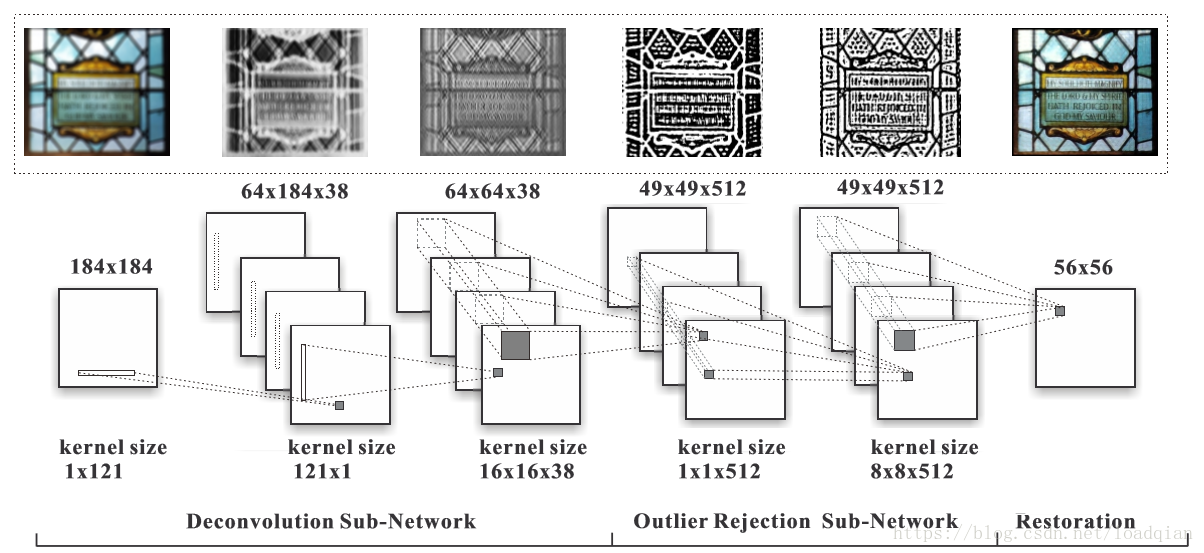
去噪CNN具有两个隐藏层,512个特征映射,输入图像卷积512内核的大16*16送入隐层中。将反卷积CNN的最后一层与去噪CNN的第一层网络相连接,合并1*1*36的核及512个16*16的核产生512个大小为16*16*36的核,在结合两个模块的时候没有非线性特征,合并后权值的数量增加,我们将对其进行微调。
训练ODCNN
我们为了训练而模糊自然图像,使用2500张自然图像,随机采样得到两百万patch。独立地训练子网络,反卷积CNN使用可分离反演初始化,其输出作为去噪CNN的输入。使用十万张184*184的小块到整个网络中进行微调,训练样本包括噪声、饱和度、压缩的小块,微调后的ODCNN的PSNR值增加了2dB,特别是对那些饱和区域。
实验和结论
本文中,我们呈现了几种反卷积结果,使用磁盘和运动内核来比较性能,平均PSNR如下表,视觉效果对比如下图:

我们的方法取得了极好的质量和视觉效果。
总的来说,我们提出了一种深度卷积网络结构来完成具有挑战性的反卷积任务,我们的主要贡献是使得传统的反卷积方法通过一系列的卷积步骤来指导神经网络和近似的反卷积,我们的系统新颖地使用了两个模块对应的反卷积和伪影去除。由于网络很难训练,采用监督的预训练方法来初始化子网络,高质量的反卷积结果证明了该方法的有效性。