凸集
定义
给定一个集合\(C \subseteq {R^n}\),满足下列条件则称为凸集
\(x,y \in C \Rightarrow tx + (1 - t)y \in C\),对于任意的\(0 \le t \le 1\) 。
从定义出发,我们也能知道非凸集的情况,下图左侧为凸集,右图为非凸集。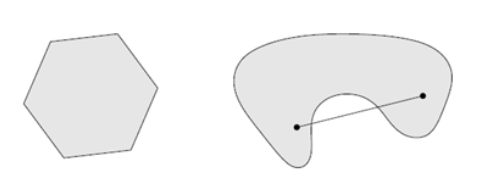
也就是说如果一个集合C是凸集,那么这个集合中任意两点之间的线段仍然在C内
凸线性组合(convex combination)
\[{x_1},{x_2}, \ldots ,{x_k} \in {R^n},\sum\limits_{i = 1}^k { {t_i} = 1,0 \le {t_i} \le 1} \]
k个点的凸组合:\({t_1}{x_1} + {t_2}{x_2} + \ldots + {t_k}{x_k}\)
凸包(convex hull)
所有元素的凸线性组合构成凸包,表示为conv(C)。convex hull总是凸的,可以直观认为凸包就是最外围的元素所围成的集合外壳,下面是两个凸包的例子: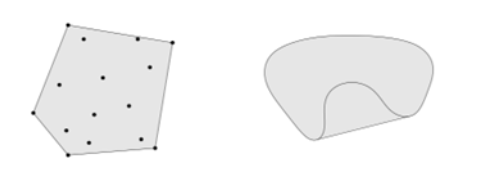
一些常见的凸集
- 空集、点、线都是凸集合
- 范数球(Norm ball): 半径为r的范数球为:\(\left\{ {x:\left| x \right| \le r} \right\}\)
- 超平面(Hyperplane): 给定任意a,b ,\(\left\{ {x:{a^T}x = b} \right\}\)
- 半空间(Half space): \(\left\{ {x:{a^T}x \le b} \right\}\)
- 仿射空间(Affine space):\(\left\{ {x:Ax = b} \right\}\)
- 多面体(Polyhedron):\(\left\{ {x:Ax \le b} \right\}\),下图为多面体
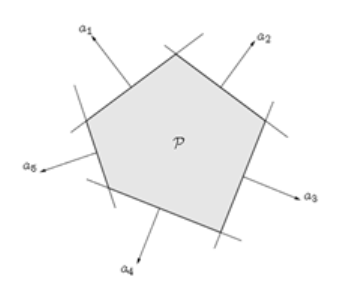
Note:集合\(\left\{ {x:Ax \le b,Cx = d} \right\}\)也是一个Polyhedron吗?
Answer:是的。因为对于任意的\({Cx = d}\),都可写成\({Cx \le d}\) 与\({ - Cx \le - d}\),这样就和\({Ax \le b}\)形式一致。
凸集的一些性质
- 可分离超平面理论(Separating hyperplane theorem):两个不相交的凸集总存在一个超平面能将两者分离,如果\(C \cap D = \emptyset \),那么总存在着a,b使得有:
\(C \subseteq \left\{ {x:{a^T}x \le b} \right\},D \subseteq \left\{ {x:{a^T}x \ge b} \right\}\)。如下图所示: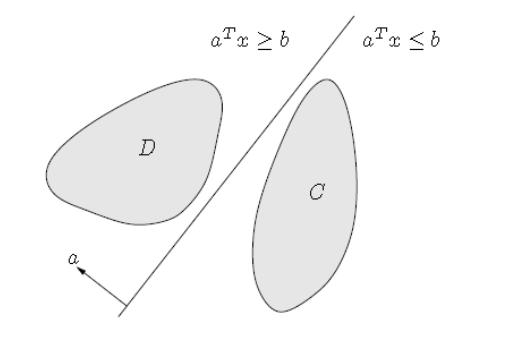
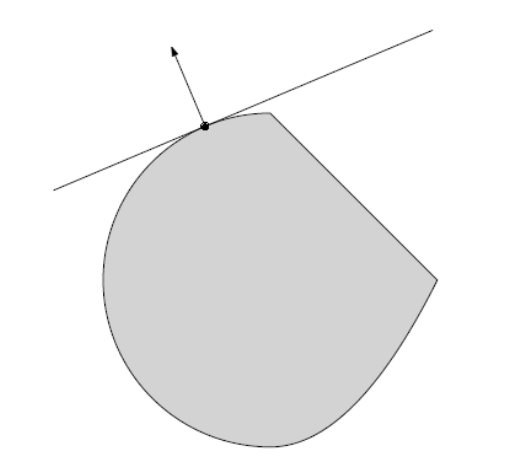
- 支撑超平面理论(Supporting hyperplane theorem):凸集边界上的一点必然存在一个支撑超平面穿过该点,即如果C都是非空凸集,\({x_0} \in bd(C)\),那么必然存在一个超平面a,使得,\(C \subseteq \left\{ {x:{a^T}x \le {a^T}{x_0}} \right\}\)。如下图:
保凸操作
- 集合交(Intersection):任何凸集之交产生的集合依旧是凸集。
- 缩放和平移(Scaling and translation):假设C为凸集,那么\(aC + b = \left\{ {ax + b:x \in C} \right\}\)对于任意a,b也是凸的。
- 仿射映射与预映射(Affine images and preimages):如果\(f(x) = Ax + b\)是凸集,那么\(f(C) = \left\{ {f(x):x \in C} \right\}\)也是凸集,如果D为凸集,那么\({f^{ - 1}}(D) = \left\{ {x:f(x) \in D} \right\}\)也是凸的。
凸函数
定义
给定映射\(f:{R^n} \to R\) 并且\(dom(f) \subseteq {R^n}\)为凸集,那么\(f(tx + (1 - t)y) \le tf(x) + (1 - t)f(y)\)对于任意\(0 \le t \le 1\),且任意\(x,y \in dom(f)\)。如下图: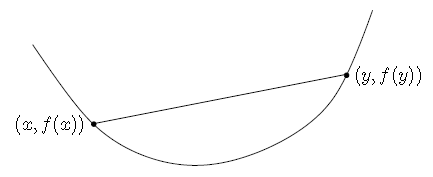
从图中可以看出,f的函数值总是位于连接f(x)和f(y)之间的直线下方。
一些常见的凸函数
- 单变量函数:
如指数函数\({e^{ax}}\)对于任意a都是凸的,幂函数\({x^a}\)在\(a \ge 1\)或\(a \le 0\)的时候为凸,当\(a \le 0\)的时候非凸,对数函数\(\log x\)是非凸函数 - 仿射函数(Affine function):
\({a^T}x + b\)既是凸函数又是非凸函数 - 二次函数(Quadratic function):
\(\frac{1}{2}{x^T}Qx + {b^T}x + c,Q \succ = 0\)(半正定)的时候为凸 - 最小平方损失函数(Least squares loss):
\(\left| {y - Ax} \right|_2^2\)总是凸的,因为展开后的\({A^T}A\)总是半正定的 - 范数(Norm):
\(\left| x \right|\)的任何范数总是凸的,\({l_p}\)范数定义为:\({\left| x \right|_p} = {(\sum\limits_{i = 1}^n {x_i^p} )^{1/p}}\),对于任意\(p \ge 1\),\({\left| x \right|_\infty } = \max \left| { {x_i}} \right|\)
谱(spectral)范数:\({\left| x \right|_{op}} = {\sigma _1}(X)\),
核范数(nuclear):\({\left| x \right|_{tr}} = \sum\limits_{i = 1}^r { {\sigma _r}(X)} \)。其中\({\sigma _1}(X) \ge \ldots \ge \sigma (X) \ge 0\)为矩阵X的从大到小排序的奇异值。 - 指示函数(Indicator function):
如果C为凸,那么其指示函数为:\({I_C}(x) = \left\{ \begin{array}{l}0,x \in C\\\infty ,x \notin C\end{array} \right.\)为凸函数。 - 最大值函数(Max function):
\(f(x) = max({x_1}, \ldots ,{x_n})\)为凸函数
凸函数的特性
- 上镜特性(Epigraph characterization):
函数f为凸函数当且仅当其上镜图\(epi(f) = \left\{ {(x,t) \in dom(f) \times R:f(x) \le t} \right\}\)为凸集,如下图: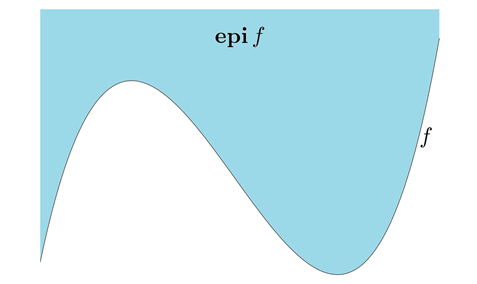
- 一阶特性(First-order characterization):
假设f处处可微,那么f为凸函数当且仅当\(dom(f)\)为凸,并且有:\(f(y) \ge f(x) + \nabla f{(x)^T}(y - x)\)对于所有\(x,y \in dom(f)\)。 - 二阶特性:
如果函数二阶可微分,则f为凸函数当且仅当\(dom(f)\)为凸,且对于所有\(x \in dom(f)\)都有\({\nabla ^2}f(x) \succ = 0\)保凸操作
- 非负线性组合
\({f_1}, \ldots ,{f_m}\)均为凸函数,那么对任意\({a_1}, \ldots ,{a_m} \ge 0\)均有\({a_1}{f_1} + \ldots + {a_m}{f_m}\)为凸。 - 逐点最大化
如果\({f_s}\)对于任意\(s \in S\)均为凸,那么\(f(x) = \max {f_s}(x),s \in S\)是凸函数。 - 部分最小化
如果\(g(x,y)\)在任意x,y处为凸函数,并且C是凸的,那么\(f(x) = \min g(x,y),y \in C\)为凸函数。