Self-supervised Image Enhancement Network: Training with Low Light Images Only
现有的图像增强数据集都是通过合成或者调整曝光时间得到的,但存在两个问题:①如何确保预先训练的网络可以用于不同设备、不同场景和不同照明条件下收集的图像,而不是构建新的训练数据集。②如何确定用于监督的正常光图像是最好的,因为相对于一张低光照图像,我们可以得到很多的正常光图像。
为了解决上述问题,本文基于信息熵理论和Retinex模型,提出了第一篇基于深度学习的完全自监督做图像增强的论文,本文提出的网络不用成对的数据集,只需要低光照图像(甚至只要一张低光照图像),训练时间为分钟级(minute-level),可以取得实时的性能。该网络将低光照图像分解为反射部分和照度部分,其中反射部分即为增强后的结果。
本文的理论来源:根据信息熵理论,直方图均匀分布的图像熵最大,信息量最大。基于这一点,本文提出了一个假设,即增强后图像最大通道的直方图分布应与直方图均衡化后的低光照图像最大通道的直方图分布一致。有了这一假设,损失函数的设计就不需要正常光图像,不仅保留了增强后图像的真实性,而且包含充足的信息。作者认为,该方法对低亮度图像的获取没有任何依赖,且训练过程完全self-supervised,因此本文提出的方法具有良好的泛化能力,即使预训练的网络对于新的环境结果不是很好,也可以通过重新训练或者微调的方式改善。
基于最大熵的Retinex模型,其理论来源如下,根据Retinex理论,图像可以分解成反射和照度部分,即
根据贝叶斯公式,可得: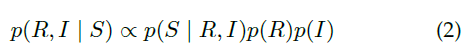
通过计算公式(2)的负对数,图像增强问题可以转化为: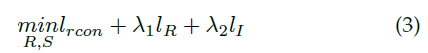
其中,重建损失定义为: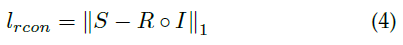
基于以下三个原因,本文提出了一个新的反射部分损失:①对于图像增强任务,处理后的图像应具有足够的信息;②处理后的图像应符合原始图像信息;③直方图均衡化可以大大提高图像的信息熵,因此反射部分损失定义为: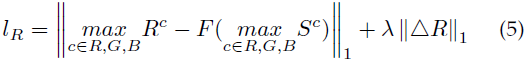
这个损失函数意味着反射率的最大通道应该与直方图均衡后低光图像的最大通道一致,并且具有最大的熵。
照度图的一个基本假设是局部一致性和结构感知。即纹理细节平滑,同时还能保持整体结构的边界。直接使用TV作为损失函数在具有强结构或亮度变化剧烈的区域失效。因为不管区域是纹理细节还是强边界,光照梯度都是均匀减少的。为了使loss感知到图像结构,用反射率梯度作为TV的加权,表示为: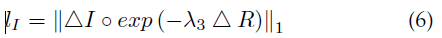
因此,可以得到以下基于最大熵的Retinex模型,用变分法或FFT来求解需要大量迭代比较耗时,为了实时对图像增强,作者将其作为损失函数,用深度学习来求解该问题。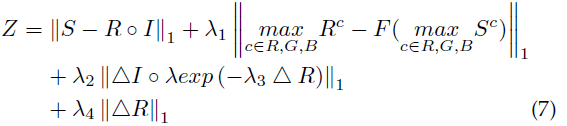
文中作者尝试了不同的网络结构,卷积层的叠加和sigmoid层就可以产生不错的结果,因此本文的网络结构设计比较简单,如下: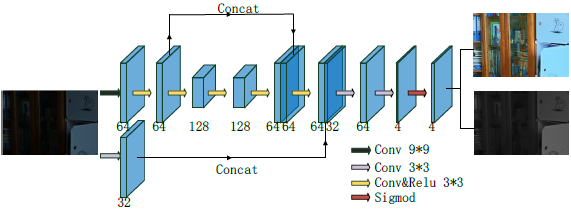
实验部分,作者采用了多种图像质量评价指标(gray entropy (GE), color entropy (CE), gray mean illumination(GMI), gray mean gradient (GMG), LOE, NIQE,PSNR, SSIM)对增强后的结果进行了验证,也做了时间上的比较,结果如下: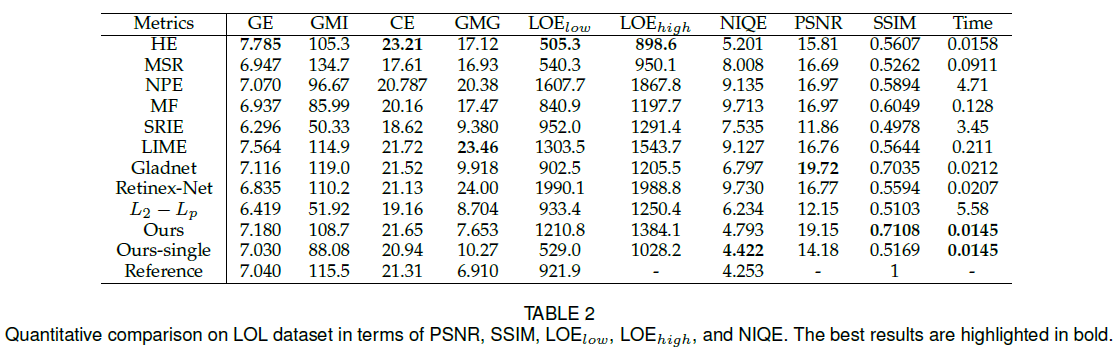
仅用一张低光照图像训练的结果如下: