第一次看强化学习的论文,可能理解不到位,如有问题,欢迎指出~
论文题目: Unpaired Image Enhancement——Featuring Reinforcement-Learning-Controlled Image Editing Software
本文的出发点:
①在大多数情况下,我们很难获取大量原始图像与增强后图像配对的数据集,因此本文提出一种不需要配对数据的图像增强网络,可以应用于真实场景。
②现有的基于CNN或者GAN的方法往往伴随着artifacts,训练高分辨率图像不稳定且耗时长,由于这些方法本质上是黑盒,不可解释也难以人为调整。
主要贡献:
为了实现无伪影、尺度不变、可解释的非成对图像增强,本文将图像编辑软件(如Adobe Photoshop)整合到GAN网络中,提出了一种以生成器作为软件控制代理的强化学习(RL)框架。不同于一般的GAN,生成器用于直接生成图像。在该框架中,生成器选择软件的参数,并在编辑结果欺骗鉴别器时获得奖励。通过使用RL进行训练,可以使用高质量的不可微图像编辑软件。作者将提出的方法应用于两个非配对的图像增强任务:照片增强和人脸美化。实验结果表明,与现有的基于非配对学习的方法相比,该方法具有更好的性能。
方法:
符号说明:
X,Y分别表示原始图像域和目标图像域, 定义数据分布为\(x\sim p_s\),\(y\sim p_t\) 。输入图像x和动作向量(action vector) \(a=[a_1,a_2,\dots,a_k]\)作为图像编辑软件S的输入,输出为编辑后的图像\(y’=S(x,a)\),在训练过程中,生成器得到的数据分布\(y’\sim p_g\)逐渐接近\(p_t\)。
整体框架:
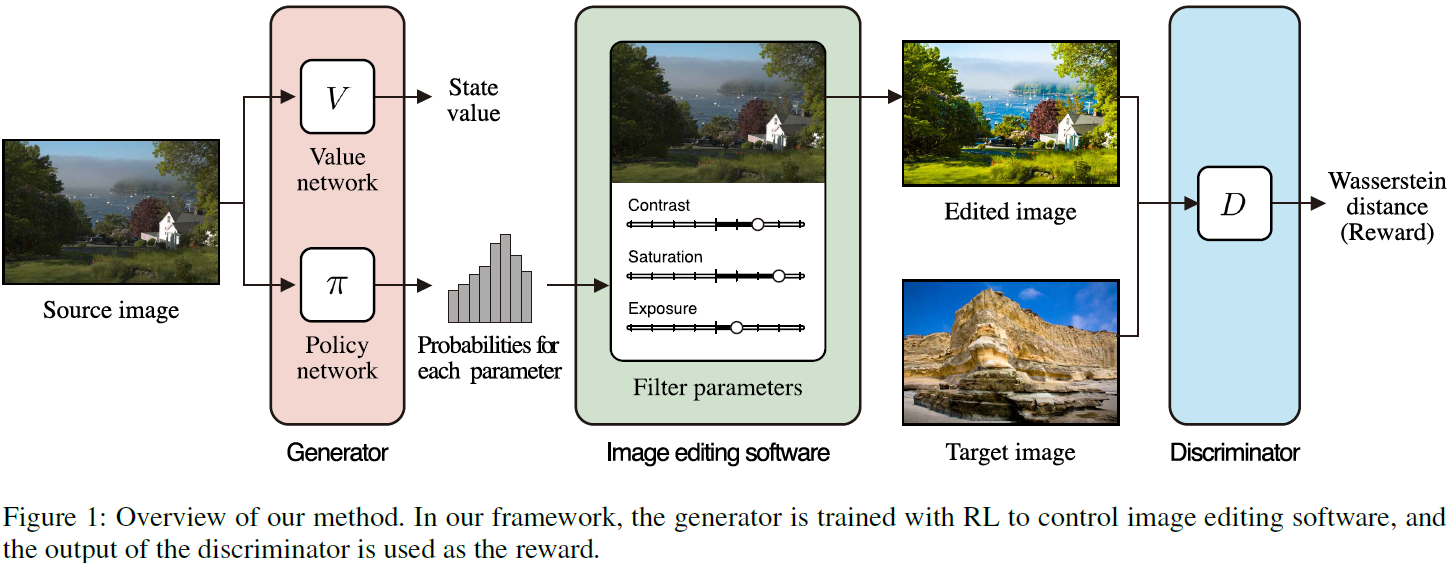
判别器:
训练过程中,本文的判别器D与一般GAN网络中的判别器作用相同,都是为了学习区分生成的图像与真实图像。这里采用梯度惩罚的Wasserstein GAN方法(WGAN-GP),判别器的损失定义为: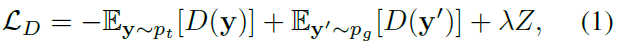
其中,Z为Lipschitz连续函数集中的正则化项,即: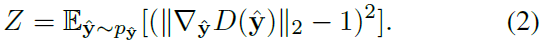
\(\hat{y}\)为是在\(p_t\)和\(p_g\)之间沿直线采样的图像。
生成器:
本文的目标是将图像编辑软件整合到GAN中,即生成器以原始图像x作为输入,输出为软件的参数。若图像编辑软件是可微的,则可直接优化如下损失函数: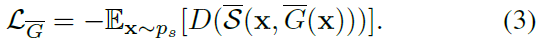
但这种方法不能应用于不可微的图像编辑软件,如PS。此外,S是非线性的函数,对于用户来说,解释序列的操作比较困难,因此作者使用single-step action。若直接使用D(y’)作为reward来欺骗判别器,可能会导致x和y’之间的不一致性,因此作者将reward定义为: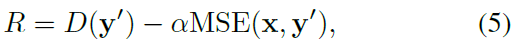
作者选择advantage actor-critic (A2C)作为RL的方法,包括值(value)网络V和策略(policy)网络\(\pi\)。其中value网络V (x)用于估计当前状态x的值,其损失定义为: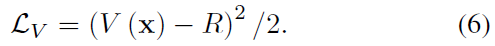
Policy网络\(\pi(a_k|x)\)输出当前状态x下每个动作\(a_k\)的概率,并经过训练使期望奖励最大化,即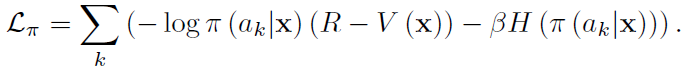
若通过a操作获得的奖励大于价值网络预测的奖励,则a的概率增加。第二项是计算熵的函数,用于鼓励代理搜索并防止收敛到局部最优。
网络结构:
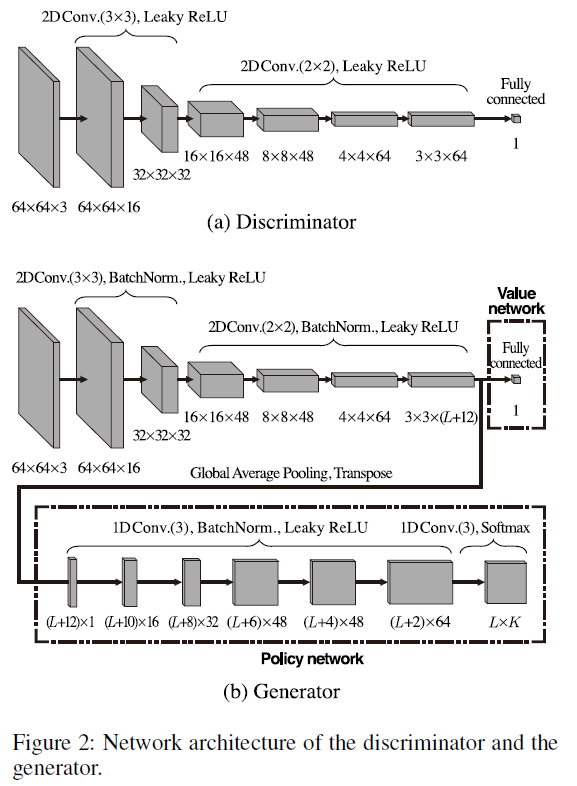
S可以取连续的参数,但选择连续动作的agent很难训练。因此,本文设计了采取离散动作的agent,策略网络输出每个离散动作概率。从上图可以看到,策略网络的输出记为q,它是一个矩阵\(R^{L\times K}\),其中L为参数的离散步长。对于每一个\(a_k\),S都有一个最大值\(a_k^{max}\)和一个最小值\(a_k^{min}\),将最大值和最小值分为L步,则策略网络对于每个动作的输出概率为: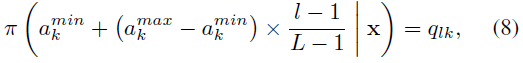
为了表示相邻离散步骤之间的关系,可以看到在策略网络最后使用了一维 (1D)卷积层使得概率q来自CNN feature。
训练和测试:
训练时将所有的图像resize成64*64,根据策略网络选择action,即\(a_k\sim\pi(a_k|x)\)将其用于编辑图像。测试时,将图像作为一个状态,然后决定性地选择action将其用于原始图像,即: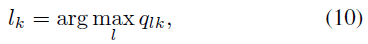
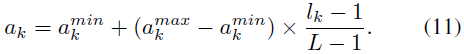
实验部分:
作者将提出的网络应用于照片增强(MIT5K dataset)和人脸美化(SCUT FBP5500 dataset),具体的实验就不详细说了,放上部分实验结果:

总结:
总的来说,这篇文章就是用强化学习的思想去学习图像编辑软件中涉及的参数设置,从而对图像进行增强或对人脸美化,使得增强的过程具有可解释性,且能运用到高分辨率的图像上。